Technical Notes
This section presents technical notes explaining thermodynamic phenomena and provides recommendations on which methods and models to use to solve problems within fluid phase behavior.
Table of contents
- 150 Years History of Cubic Equations of State
- What Causes Asphaltenes to Precipitate and How is it Modeled?
- Stages of Carbon Capture Storage
- Absolute Enthalpy The Key to Accurate Depth Gradient Simulations
- New Book on Phase Behavior of Petroleum Reservoir Fluids
- EoS Modelling with the Critical Point as Anchor Point
150 Years of History of Cubic Equations of State
After van der Waals presented the first cubic equation of state in 1873, it took more than 100 years for cubic equations to become the invaluable tool in the petroleum industry they are today. This had several reasons, one being that the early petroleum industry did not need such a tool. The need arose when the production of gas and oil from deep reservoirs at high pressures and temperatures took off in the 1970s, but there were still obstacles to be overcome. New algorithms had to be developed to calculate phase amounts and phase compositions throughout the PT region, including the near-critical region. Since cubic equations were developed for hydrocarbon mixtures, they were not in their original form applicable to mixtures with water and other polar components. The gap between the equations of state and the models used in the chemical industry for mixtures with polar components had to be closed. This technical note tells the story of cubic equations and what has made a 150-year-old model concept survive and remain unsurpassed.
In 1873, Johannes Diderik van der Waals defended his doctoral thesis entitled: “On the Continuity of the Liquid and Gaseous States” [1], in which he argued that the properties of a pure component in both the gaseous and liquid states are determined by the location of the critical point. This was only four years after the existence of a critical point had been documented [2] and at a time when it was not yet fully accepted that fluids are made up of molecules. Scientists still considered the gas and liquid states to be independent. It must have required an eminent physical understanding and a certain degree of courage to put forward a theory that there is a continuity between the gas and liquid states. As illustrated in Figure 1, van der Waals claimed that gas and liquid coexist at the vapor pressure thanks to a balance between repulsive and attractive molecular forces. The gas phase is dominated by repulsive forces, and the liquid phase by attractive forces. Moving up the vapor pressure curve towards the critical point, the molecular forces in the two phases gradually become more similar, and at the critical point the two phases are identical. At pressures and temperatures higher than at the critical point, a phase separation can no longer occur.

Figure 1 How van der Waals saw the gas and liquid densities develop with temperature.
van der Waals expressed his findings in the equation shown in Figure 2. It says that the pressure is determined by two opposing molecular interactions, one repulsive and one attractive. The repulsive term is a slight modification of the ideal gas equation, while the attractive term expresses that two molecules will attract each other with a force that increases with the inverse of the squared molar volume, V.

Figure 2 Van der Waals equation of state [1].
Figure 3 shows qualitative PV curves at three different temperatures. At temperatures, T, higher than the critical temperature, Tc, the PV curve has a hyperbolic-like shape known from the ideal gas equation. At Tc the PV curve has what van der Waals interpreted as an inflexion point at the critical pressure, Pc. This made it possible to express the parameters a and b as unique functions of Tc and Pc, thus expressing van der Waals’ main point, that the properties of a pure component in the entire PT region are determined by the location of the critical point. At temperatures lower than Tc, the PV curve has a horizontal section where a reduction in volume does not change the pressure. On this horizontal section, gas and liquid coexist, and a phase transition from gas to liquid takes place. The van der Waals (vdW) equation cannot represent the horizontal part of the phase diagram (dashed in Figure 3), but it represents the endpoints and thus the molar volumes of the gas and liquid phases present during the phase transition. The vdW equation can be rewritten as a third-degree equation in molar volume and is therefore also called the first cubic equation of state. In 1910 van der Waals received the Nobel prize for his work on this equation.

Figure 3: PV isotherms of a pure component at three different temperatures.
For many years, the vdW equation was more of an academic discovery than a practical tool. The application was limited to pure components, and the accuracy was not considered sufficient for use in engineering calculations. In 1949, Redlich and Kwong (RK) [3] presented a slightly modified cubic equation of state. They were the first to suggest how to extend the use of a cubic equation of state to multi-component mixtures. The different molecules were represented as one average molecule as sketched in Figure 4. This was a major step forward and the RK equation is considered the first modern cubic equation of state.

Figure 4 The essence of the mixing rules for cubic equations of state.
Today, the Soave modification (SRK) from 1972 [4] is more widely used than the RK equation. Soave found that the variation of the vapor pressure with temperature was more curved than predicted by the vdW and RK equations. A few years earlier, Pitzer had introduced the acentric factor [5] as a measure of the curvature of a vapor pressure curve relative to that of argon. Soave modified the curvature of the vdW vapor pressure curve by making the a-parameter a function of a 2nd order polynomial in the acentric factor. Soave’s equation is shown in Figure 5.

Figure 5 Soave-Redlich-Kwong (SRK) equation [4].
Figure 6 illustrates Soave’s correction to the vapor pressure curve that makes use of the acentric factor.

Figure 6 Soave’s modification to the vdW vapor pressure curve [4].
Inorganic components like N2, CO2 and H2S often appear in petroleum reservoir fluids. These components have strong mutual attractive forces, while the interaction is less between an inorganic component and a hydrocarbon. To better describe the interaction between inorganics and hydrocarbons, Soave introduced a correction to the a-parameter called a binary interaction parameter, kij. For a component pair consisting of a hydrocarbon and an inorganic component, kij is typically in the range 0.04-0.15.
Soave’s equation predicted too low liquid densities. In 1976 Peng and Robinson (PR) proposed a modified cubic equation of state [6] that reduced the discrepancy seen with the SRK equation between experimental and calculated liquid densities, but it was not until 1982 satisfactory results for liquid densities were obtained with a cubic equation of state. As illustrated in Figure 7, Peneloux [7] obtained accurate liquid densities by horizontally shifting the PV curves by a distance, c, to have them match experimental liquid molar volumes.

Figure 7 Volume translation concept by Peneloux et al. [7].
Figure 8 shows how the SRK equation and the Peneloux (Pen) volume-corrected equation are related.

Figure 8 Relation between SRK equation [4] and Peneloux volume corrected equation [7].
Accurate phase densities are essential, but the most important application of an equation of state is to calculate the amounts and compositions of two or more phases in equilibrium. At equilibrium, all components in each phase will have the same fugacity, f. The left-hand container in Figure 9 shows a system that is not in equilibrium. All components in the gas phase have a higher fugacity than the same components in the liquid phase, and there is a net transport of components from the gas phase to the liquid phase. Fugacity can be seen as a measure of the tendency to escape. In the right-hand container, all components have the same fugacity in both the gas and liquid phases, and there is no net transport across the phase boundary. The fluid system is in equilibrium.

Figure 9 Non-equilibrium system (left-hand) and equilibrium system (right-hand).
Carl von Linde, the founder of the Linde chemical company, became familiar with the van der Waals equation as early as 1871/72, which was before van der Waals published the equation, and he tried to use the equation to solve multi-component phase equilibrium problems [8]. He had to give up because the calculations were so cumbersome that he found it almost impossible to solve them manually. The availability of computer power was one of the reasons the use of cubic equations of state took off in the late 1970s.
Even after computers became available, it was unclear how to determine whether a fluid system would remain single-phase or split into two or more phases. Gibbs had already described a procedure for this around 1900 [9]. Among the possible states, a fluid system will choose the one with the lowest Gibbs energy. However, Gibbs did not have the computational tools needed to make full use of his discovery, and it went almost unnoticed until Professor Michelsen in the early 1980s became aware of it and used it to develop efficient computer algorithms [10].
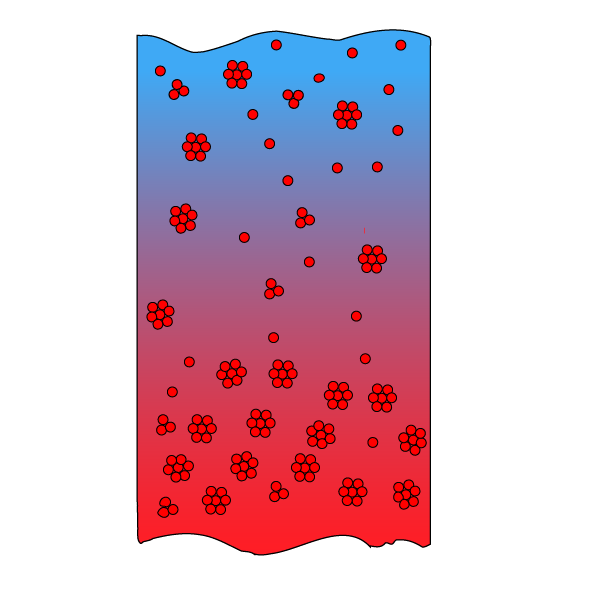
Water is often produced together with oil and gas. Some of the water may have been dissolved in the hydrocarbon phases in the reservoir, and some may come from an underlying formation water zone. Cubic equations were long considered unsuitable for handling mixtures with water because water is a polar component with strong mutual attractive forces. As shown in Figure 10, water molecules dissolved in a hydrocarbon (HC) phase will not be evenly distributed but stick together and form H2O-rich pockets. The figure also shows that something similar is seen for hydrocarbons dissolved in a water phase. The classical mixing rules shown in Figure 5, assume that all molecules are distributed evenly in both gas and liquid phases.

Figure 10 Close-up of molecules in a hydrocarbon phase saturated with water and in a water phase saturated with hydrocarbons. Mixing rule of Huron and Vidal for the a-parameter.
At the time cubic equations became frequently used in the oil industry, the chemical industry had already for several years successfully been using so-called GE models that could handle mixtures with polar components. These models describe what difference it makes to the interaction between two molecules whether they are identical or not. The GE models had the drawback that they were limited to liquid phases and low pressure. They were therefore not immediately applicable in the petroleum industry.
Models were proposed that incorporated the qualities of a GE model into a cubic equation of state, but most of them had the disadvantage that they required interaction parameters to be determined for all pairs of dissimilar molecules, and it could not be guaranteed that a calculation with negligible amounts of water would converge towards the result that would be obtained for a water free mixture using classical mixing rules. A publication by Huron and Vidal [11] stood out. The attractive term, a, had been rewritten to be a function of GE at infinite pressure (see Figure 10) in such a way that new interaction parameters were only required for component pairs with water or another polar component.
This is where the story of cubic equations of state ends for now. Cubic equations of state have undergone a great deal of development since 1873, so one may wonder why the van der Waals equation continues to be referred to. This is because van der Waals was the first to realize that the location of the critical point of a fluid exerts a decisive influence on the phase behavior, not only near the critical point, but throughout the gas and liquid regions. None of the improvements to the original equation described above have challenged this assumption.
References
- van der Waals, J.D., “O ver de Continuiteit var der Gas- en Vloeistoftoestand”, Doctoral Dissertation, Leiden University, The Netherlands, 1873 (In Dutch).
- Andrews, T. “On the Continuity of the Gaseous and Liquid States of Matter”, Philosophical Transactions of the Royal Society of London, vol. 159, 575–590, 1869.
- Redlich, O. and Kwong, J.N.S., “On the Thermodynamics of Solutions. V. An Equation of State. Fugacities of Gaseous Solutions”, Chem Review 44, 233-244, 1949.
- Soave, G., “Equilibrium Constants from a Modified Redlich-Kwong Equation of State”. Chem. Eng. Sci. 27, 1197-1203, 1972.
- Pitzer, K., “Volumetric and Thermodynamic Properties of Fluids. I. Theoretical Basis and Virial Coefficients”, J. Am. Chem. Soc. 77, 3427-3433, 1955.
- Peng, D,-Y. and Robinson, D.B., “A New Two-Constant Equation of State”, Ind. Eng. Chem. Fundam. 15, 59-64,1976.
- Péneloux, A., Rauzy, E. and Fréze, R., “A Consistent Correction for Redlich-Kwong-Soave Volumes”, Fluid Phase Equilibria 8, 7-23, 1982.
- Burr, P. et al. “Professor Michelsen’s Impact on Physical Property Prediction at Linde Engineering and Ideas for Future Directions”, Fluid Phase Equilibria 580, 114019, 2024.
- “The Collected Works of J. Willard Gibbs”, Nature 124, 119–120, 1929.
- Michelsen, M.L., “The Isothermal Flash Problem, Part I. Stability. Part II. Phase-Split Calculation”, Fluid Phase Equilibria 9, 1-41, 1982.
- Huron, M.J. and Vidal, J., “New Mixing Rule in Simple Equations of State for Representing Vapor-Liquid Equilibria of Strongly Non- Ideal Mixtures”, Fluid Phase Equilibria 3, 255-271, 1979.
What Causes Asphaltenes to Precipitate and How is it Modeled?





dG=VdP-SdT
G is Gibbs free energy, V is molar volume, S is entropy, and T is temperature. A change from a single-phase fluid to a two-phase fluid will occur if the Gibbs free energy of the fluid when split into two phases is lower than the Gibbs free energy, the fluid would have as a single-phase. At a fixed temperature, the last term in the above relation cancels out and the optimum state after a pressure reduction (negative dP) is the one (single-phase or two-phase) of the higher molar volume. This means that the asphaltene onset pressure is determined by the system parameters that are most influential on the total molar volume.
Figure 3 illustrates the two options that exist for an asphaltene-containing oil when the pressure drops. It can remain single-phase, or it can split into two phases, with the incipient phase being dominated by asphaltenes. The state of the higher volume is the stable one.

For any reservoir fluid, reducing the pressure at a constant temperature will make the volume increase, and so will the spacing of the molecules that make up the fluid. As illustrated in Figure 4, asphaltene precipitation will occur when the distance between the oil molecules becomes too large to keep the asphaltene molecules in solution.

One may ask whether this mechanism is consistent with the fact that resins are seen to play an important role in asphaltene precipitation. Resins are aromatic compounds and have a higher density (smaller intermolecular distance) than other hydrocarbon groups (paraffins and naphthenes), and it is primarily this property that makes reservoir fluids rich in resins less likely to precipitate asphaltenes.
For the oil industry, it is desirable to use the classical cubic equations of state for as many purposes as possible, as these equations are the industry standard. A recent paper [1] has shown that to date, no asphaltene data has been published that could not be satisfactorily modeled with a classical cubic equation of state. There is no need for more complex equations, such as CPA or PC-SAFT. Figure 5 shows examples of experimental asphaltene onset pressure data for Type A-D fluids along with simulation results with the SRK equation. Data sources and model parameters can be seen from the paper or obtained by contacting Kapexy Aps.




- [1] Pedersen, K. S., “The Mechanisms Behind Asphaltene Precipitation – Successfully Handled by a Classical Cubic Equation”, SPE-224534-MS, Gas and Oil Technology Showcase and Conference, Dubai , April 21-23, 2025.
Stages of Carbon Capture Storage
CO2 has several industrial uses, including supercritical extraction, fire extinguishing, refrigeration, and welding. Thanks to these many applications, data and validated models for CO2 are freely available on the Internet. In that light, one may wonder why Carbon Capture Storage (CCS) has developed into a new technical discipline that engages many engineers worldwide. It has because CCS involves transport and storage of CO2 quantities that are out of proportion to the amount of CO2 seen in industrial applications and takes place under other conditions. The weight of CO2 produced by burning fossil fuels is three times the weight of the fossil fuels being burned and amounted to 37.4 Gt in 2023. Over the years, the oil industry has built up reliable simulators for the production, transport and processing of large quantities of gas and oil, as well as for injecting gas into depleted oil fields. It seems natural to use the same models and methods to simulate CO2 transport and underground storage. However, CO2 differs from oil or gas and presents challenges not seen for hydrocarbon mixtures. This note reviews some of the characteristics of CO2 and some of the challenges that arise with CCS, but it starts with a historical review of the CO2 concentration in the atmosphere.
CO2 concentration in the atmosphere
Seen over a period of millions of years CO2 has an interesting and life-giving history. Without CO2, there would not have been the kind of life on earth we see today. The atmosphere today consists of about 78.08% nitrogen (N2), 20.95% oxygen (O2), 0.93% argon (Ar) and 0.04% (about 400 ppm) CO2, but it has not always been like that. The atmosphere would have contained no O2, had it not been formed by the photosynthesis of green plants, and without that more than 21% (210,000 ppm) of atmospheric air would have been CO2, disregarding the water content. From the day green plants arose around 700 million years ago, they began to consume CO2, which as shown in Figure 1 was used as a building material to form glucose (C6H12O6) and oxygen (O2). This process is called photosynthesis. For plants, O2 is a waste product, but the animals and humans who later populated the earth reversed the chemical reaction in Figure 1 by consuming plants and other animals. This released CO2, which in turn could be used as building material by the plants.
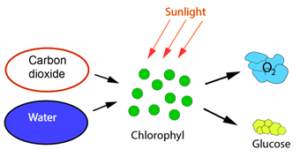
Figure 1 Photosynthesis.
Not all organisms are consumed by other organisms. Some are buried underground and over time turned into gas, oil, or coal. With each organism buried, humans and animals were giving less CO2 back to the atmosphere than consumed. A hundred years ago, the CO2 concentration in the atmosphere had dropped to about 280 ppm (0.028%). A drop in atmospheric CO2 concentration from more than 210,000 ppm when green plants appeared to around 280 ppm may seem quite dramatic but given that it happened over a period of about 700 million years, the annual decrease in CO2 concentration is only of the order of 0.3 parts per billion and has hardly been felt within a few generations. With a continued steady annual decline in CO2 concentration, it would take about a million years for the CO2 to be used up and all life would die out.
Throughout history, there have been fluctuations in the CO2 concentration in the atmosphere. Measurements suggest that the CO2 concentration during the last glacial period, about 20,000 years ago, was as low as 180 ppm. Cold water can dissolve more CO2 than hot water. Degassing of CO2 from seawater is therefore believed to be a major source of the increase in CO2 concentration in the atmosphere from about 180 ppm to 280 ppm that happened from the time about 30% of the earth was covered by ice to the start of the modern industrial age about 100 years ago.
CO2 is produced when burning methane (CH4), other hydrocarbons, and coal. This could be seen to bring some of the CO2 originally in the atmosphere back to the atmosphere. However, if more CO2 is produced from respiration of living organisms and by burning fossil fuels than consumed by plants and trees, the CO2 concentration in the atmosphere will increase as opposed to what has happened for the millions of years with a net removal of CO2 from the atmosphere to carbon compounds buried underground. If all the carbon were taken up from the underground and burned, one must expect the CO2 concentration to return to the 21% level it had when the first green plants appeared, in which environment no animal species would survive.
CO2 quantities produced by combustion
The chemical reaction for burning of methane (CH4) is:
CH4 + 2O2 → CO2 + 2H2O
Table 1 shows a typical reservoir oil composition. As is detailed in the table, burning 1 mole (=107.96 g) of oil will produce 344.18 g CO2. The weight amount of CO2 produced is in other words 344.18/107.96 = 3.19 times higher than the weight amount of the reservoir oil.
| Oil
component |
Mol%
of oil |
Molecular
weight |
Grams oil constituent
per mole oil |
Grams carbon
per mol oil |
Grams CO2
produced per mole oil |
| N2 | 0.56 | 28.01 | 0.16 | 0.00 | 0.00 |
| CO2 | 3.55 | 44.01 | 1.56 | 0.43 | 1.56 |
| C1 | 45.33 | 16.04 | 7.27 | 5.44 | 19.94 |
| C2 | 5.48 | 30.07 | 1.65 | 1.31 | 4.82 |
| C3 | 3.70 | 44.10 | 1.63 | 1.33 | 4.88 |
| iC4 | 0.70 | 58.12 | 0.41 | 0.34 | 1.23 |
| nC4 | 1.65 | 58.12 | 0.96 | 0.79 | 2.90 |
| iC5 | 0.73 | 72.15 | 0.53 | 0.44 | 1.61 |
| nC5 | 0.87 | 72.15 | 0.63 | 0.52 | 1.91 |
| C6 | 1.33 | 86.18 | 1.15 | 0.96 | 3.51 |
| C7+ | 36.11 | 254.86 | 92.03 | 82.31 | 301.80 |
| Total | 107.96 | 93.87 | 344.18 |
Table 1 Oil compositions and weight amount of CO2 produced by burning 1 mole of oil.
At reservoir conditions, CO2 and the oil in Table 1 will have approximately the same density. The CO2 formed by burning 1 reservoir cubic meter of oil will thus occupy a volume of around 3 cubic meters at reservoir conditions. As sketched in Figure 2, storing CO2 in depleted oil fields will therefore only provide space for one third of the CO2 produced. If the CO2 concentration in the atmosphere is not to increase, space must be found elsewhere for two thirds of the CO2 produced.
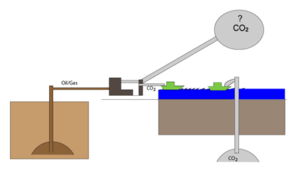
Figure 2 Illustration of the fact that depleted oil reservoirs can only hold a third of the CO2 produced by burning oil and gas.
CO2 capture
The oxygen (O2) needed for the combustion of gas and oil comes from atmospheric air. Table 2 shows the compositions of atmospheric air and of a typical combustion gas.
| Component | Atmospheric Air
Mol% |
Combustion Gas
Mol% |
| N2 | 78.08 | 66-71 |
| O2 | 20.95 | 2-3 |
| Ar | 0.93 | 0.7 |
| CO2 | 0.04 | 8-10 |
| H2O | 18-20 |
Table 2 Composition of atmospheric air and a typical combustion gas.
Before CO2 is disposed of, it must be separated from N2 and other gases. This can be done using an amine absorption process as sketched in Figure 3. CO2 is absorbed when the combustion gas contacts the amine (MEA) solution, while N2 and other gases are discharged at the top. The absorbed CO2 is separated from the amine solution in a heater.
The chemical reactions are:
Absorption:
MEA + CO2 → MEACOO– + H+
Bicarbonate formation:
MEACOO– + H2O → MEA + НСO–3
Desorption:
HCO–3 + H+ → CO2 + H2O
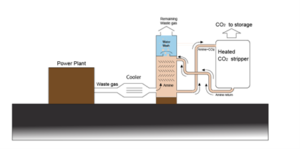
Figure 3 Amine absorption unit for separating CO2 from other gases contained in combustion gas.
CO2 at pipeline and storage conditions
Figure 4 shows the phase diagram of CO2. The CO2 molecule is linear, which in both the liquid and the vapor state favors a high density. The linear shape is also the reason CO2, compared to other components of approximately the same molecular weight, solidifies at a higher temperature.
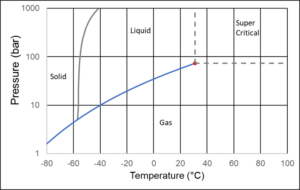
Figure 4 CO2 phase diagram.
Ship transport of CO2 will most often take place with CO2 placed in insolated cryogenic tanks, where the temperature is around -46°C and the pressure high enough to ensure that the CO2 is in liquid form, which means 8 bar or slightly higher. In a pipeline, the temperature will be determined by the ambient temperature, which will often be 4-30°C. The pressure is adjusted to ensure the density is high, without requiring an unreasonable compressor capacity. This is achieved at a pressure of 80-150 bar. Underground storage of CO2 in depleted oil fields or in aquifers could take place at a temperature of around 75°C and a pressure of around 225 bar.
Figure 5 shows the density of CO2 at typical shipping, pipeline and aquifer conditions. In marine transport, the CO2 density exceeds that of pure water, while at pipeline conditions the density is slightly lower, but still high considering that it is a condensed gas component. At aquifer conditions, CO2 is supercritical, but the density is still relatively high.
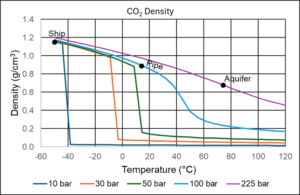
Figure 5 CO2 density at typical shipping, pipeline, and aquifer conditions.
Pipeline transport of CO2
In a pipeline, it is preferable to transport CO2 as single-phase liquid, but two-phase transport may occur. If so, it will be at temperature and pressure conditions located somewhere on the vapor pressure curve in Figure 4. This is a major difference compared to gas and oil mixtures, for which the two-phase region may cover a large PT area. This does not mean that the change from gas to liquid is instantaneous in a pipeline transporting CO2. Both gaseous and liquid CO2 can be present over long pipe distances, possibly in the entire pipe.
When carrying out flow simulations for a pipeline transporting gas and oil, it is for each section calculated how the heat (enthalpy) exchanged with the surroundings affects the relative phase quantities, their composition, and the temperature in the pipeline. This can either be done by table look-up or by continuously calculating how the phase quantities and compositions at the current pressure change with temperature. That method cannot be used for pure CO2. For a given pressure, the temperature remains fixed as long as two phases are present.
Figure 6 shows a Pressure-Enthalpy diagram for CO2. If two phases exist at a temperature of 10°C, the pressure is approximately 45 bar. The liquid phase will have an enthalpy of around -260 kJ/kg and the gas phase an enthalpy of around -63 kJ/kg. The total fluid will have an enthalpy in that range and the relative amounts of gas and liquid are determined using the lever rule.
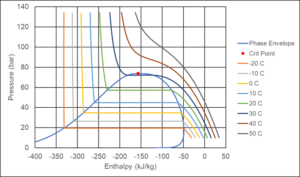
Figure 6 Pressure-Enthalpy (PH) diagram for CO2. The enthalpy reference state is ideal gas at 0°C.
Should a leak occur on a pipeline transporting natural gas, the leaking gas will rise into the air because the molecular weight of natural gas (18-20) is lower than that of atmospheric air (around 28.964). CO2 has a molecular weight of 44.0 and it will take time before the leaking CO2 mixes with the atmospheric air. In calm weather, CO2 from a leaking CO2 pipeline could form a kind of blanket around the leak and pose a hazard to people nearby.
Thermodynamic properties of pure and lightly polluted CO2
Thanks to the many industrial uses of CO2, good, validated, and easily accessible models exist for describing the properties of CO2. The volume-corrected SRK and PR equations are the industry standard for oil and gas and can also be used for CO2. In case more accurate CO2 properties are needed, one may use the Span-Wagner equation [1] developed for pure CO2, or the GERG-2008 equation [2]. The latter can handle mixtures of up to 20 specific components including CO2.
The CO2 to be transported and stored underground will seldom be pure CO2. Figure 7 shows the phase diagram of CO2 with trace amounts of nitrogen, argon, and water. It illustrates the fact that liquid water may well form in a pipeline transporting lightly polluted CO2. This may lead to corrosion problems as dealt with later. The industry standard SRK and PR equations are also applicable to mixtures with water, but it requires modifications capable of describing that water molecules when mixed with other components do not distribute randomly but prefer other water molecules as their nearest neighbors. Such modifications of the classical cubic equations are well described in the literature [3a].
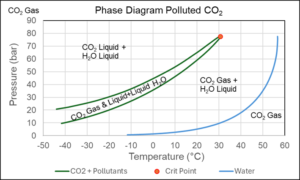
Figure 7 Phase diagram of mixture consisting of 97.7 mol% CO2, 1.6 mol% N2, 0.3 mol% Ar, and 0.4 mol% H2O.
Even trace amounts of water can lead to the formation of CO2 gas hydrate. This is a solid with properties similar to ice that can form at temperatures significantly higher than 0°C, which is the freezing point of water. Figure 8 shows a phase diagram for CO2 with trace amounts of water. As is seen from the figure, gas hydrate formation will only occur if some CO2 is in gaseous form, or the temperature is lower than around -13°C.
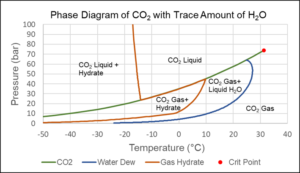
Figure 8 Phase diagram of mixture 99.9 mol% CO2 and 0.1 mol% H2O.
CO2 storage in depleted oil fields
The most obvious storage sites for the CO2 produced by burning oil and gas from petroleum reservoirs are the same reservoirs after the production by natural depletion has stopped. CO2 gas injection into oil fields has for many years been used as an enhanced oil recovery (EOR) technique. The injected CO2 mixes with the oil left in the depleted field and forms a zone that propagates through the field and pushes the oil forward towards the production well. It is a known and safe technique as long as the pressure in the reservoir does not exceed the original reservoir pressure. The mechanisms behind miscible gas displacement are well documented [3b]. Although this is an obvious storage option, additional storage space must be found because, as already mentioned, the CO2 produced takes up three times the volume that the produced oil or gas leaves in the reservoir.
CO2 storage in aquifers
The term Carbon Capture and Storage (CCS) was first used in the early 2000s. It was the time, it became clear that a new technical discipline was needed if virtually all CO2 from combustion gases were to be captured and purified, and sufficient storage space were to be found for the purified CO2. Brine reservoirs are present in large numbers worldwide and could be candidates to provide the additional storage capacity needed beyond that found in depleted oil fields.
The solubility of CO2 in saltwater is much lower than in oil. As illustrated in Figure 9 an aquifer volume of around 50 m3 would be needed if the CO2 produced by burning 1 reservoir cubic meter of oil were to dissolve in a brine aquifer [4].
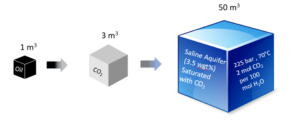
Figure 9 Volumetric development from oil at reservoir conditions to CO2 at reservoir conditions to CO2 dissolved in a brine aquifer.
According to the International Energy Agency, CO2 emissions in 2023 from the combustion of fossil fuels were 37.4 billion tons. If this much CO2 were to dissolve in a 200 m thick aquifer with a porosity of 20%, an aquifer area of the order of 20,500 square km would be needed. This is 47% of the area of Denmark. It seems unrealistic to find storage capacity in brine aquifers of that order of magnitude every year. Most of the CO2 stored in the brine aquifers will therefore remain in the form of free CO2 with some water content (a so-called CO2 plume). When assessing the storage capacity of a brine aquifer, permeability and mechanical strength of the rock material are therefore more important than the CO2 solubility in brine.
Risk of dissolution of rock material
Chalk and limestone are frequently occurring underground rock materials and consist of calcium carbonate (CaCO3). CO2 dissolved in water (H2O) can dissolve calcium carbonate by converting it to calcium and hydrogen carbonate ions:
CaCO3 + CO2 + H2O → Ca++ + 2HCO–3
Each mole of CO2 (44 g) that dissolves in water can dissolve one mole of calcium carbonate (100 g). If the production of CO2 in 2023 of 37.4 billion tons were injected into a limestone reservoir with a porosity of 20% and the size of Denmark (42,952 km2), it would lead to the land surface sinking by 0.9 meters.
The dissolution issue is not limited to chalk and limestone. Most sandstone has a high concentration of potassium feldspar (KAlSi3O8), which may also dissolve or at least corrode when contacted with CO2 rich water.
If CO2 is stored in a rock material whose main components are insoluble in CO2-rich water, there will not be a risk of collapse, but CaCO3 could be the material that binds the rock together. If the binding material dissolves, CO2 might leak to the atmosphere.
Corrosion problems in pipelines transporting CO2
Transport of CO2 carrying water can cause corrosion problems in an iron pipeline. Dissolved in water, CO2 will form carbonic acid (H2CO3), which can react with iron to form iron carbonate (FeCO3). If the FeCO3 layer adheres well to the iron surface, it can act as a physical barrier limiting further corrosion. Otherwise, the iron may react with the hydroxide ions (OH–) in the water to form iron hydroxide (Fe(OH)2), which in the presence of oxygen can be oxidized to iron oxide (Fe2O3), commonly known as rust.
CCS in a nutshell
Although CO2 is a well described component, the need has arisen for a new CO2 discipline called CCS. The reason is that the amount of CO2 that needs to be handled and disposed of is far larger than seen in any industrial use of CO2. The mass of CO2 produced is three times the mass of the burned gas and oil. CCS only makes sense if its energy consumption is significantly less than the energy obtained by burning the corresponding amount of fossil fuels. It will save money if the infrastructure and the simulation models that already exist for the transport and production of oil and gas can be reused. However, CO2 differs in several respects from oil or gas. The two-phase area of purified CO2 is much narrower than what the oil and gas flow and reservoir simulators are designed for. Dissolved in water, CO2 acts as an acid that can cause problems with corrosion in pipelines and lead to the dissolution of the rock formation in chalk and limestone aquifers with the risk of the ground sinking or CO2 escaping into the atmosphere.
References
[1] Span, R. and W. Wagner (1996), A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple-Point Temperature to 1100 K at Pressures up to 800 MPa, J. Phys. Chem. Ref. Data 25, 1509.
[2] Kunz, O. and Wagner, W., The GERG-2008 Wide-Range Equation of State for Natural Gases and Other Mixtures: An Expansion of GERG-2004, Journal of Chem & Eng Data 57, 2012, 3032-3091.
[3] Pedersen, K.S., Christensen, P.L. and Shaikh, J.A., Phase Behavior of Petroleum Reservoir Fluids, 3rd Edition, Chapters 15[b] and 16[], Taylor & Francis, Boca Raton, FL, 2024.
[4] Pedersen, K.S. and Christensen, P.L., CO2 Solubility in Brine Aquifers – Volumetric Considerations, Paper OTC-34849-MS presented at the Offshore Technology Conference Asia, Kuala Lumpur, February 27 – March 1, 2024.
Absolute Enthalpy The Key to Accurate Depth Gradient Simulations
The absolute enthalpy is needed in simulations of how a temperature gradient affects the variation in fluid composition with depth in a petroleum reservoir. Enthalpy is a thermodynamic property used in heat exchange calculations, which is a topic most engineering students are exposed to in college. However, the enthalpy you practice in college is relative to a reference state. The absolute enthalpy is more complex and less accessible. No simple method exists to determine the absolute enthalpy, but as explained in this note, it is possible to determine the absolute enthalpy of reservoir fluid constituents from detailed and accurate depth gradient data. This enables reliable simulations of the compositional variation with depth in a new field if just one fluid sample exists, and the vertical temperature gradient is known. Minor adjustments can easily be made to get an exact match of the depth of an observed gas-oil-contact (GOC) or to finetune the variation in GOR with depth.
The enthalpy (H) is defined as
H = U+PV
where U is the internal energy, P is pressure and V is molar volume. In 1848, Lord Kelvin defined 0 K as the temperature at which molecules no longer move. This does not mean that their internal energy is zero at 0 K. While only of theoretical interest in classical heat transfer calculations, the internal energy at 0 K and the evolution of the internal energy at higher temperature do count when assessing compositional changes with depth in an oil reservoir with a vertical temperature gradient.
The absolute enthalpy can be expressed as
Habs = Habs,ig + Hres
where ig stands for ideal gas and res for residual. The ideal gas enthalpy represents the energy inside a molecule (intra molecular energy), while the residual enthalpy originates from molecular interactions. The residual enthalpy can be calculated with an equation of state and will not be further discussed. At 0 K, the internal energy is at a minimum. At a higher temperature, the internal energy and the ideal gas enthalpy will increase as polyatomic molecules will vibrate and rotate around their center of gravity.
Since no intermolecular interactions are involved for an ideal gas, the total ideal gas enthalpy of a multi-component mixture can be found as the molar average of the ideal gas enthalpies of the individual components. To evaluate how much the enthalpy of a 5-component ideal gas mixture changes from a temperature T1 to a temperature T2, two different paths can be followed. As illustrated by the two upper bar diagrams in Figure 1, one is to evaluate the absolute ideal gas enthalpies at the two temperatures and subtract the absolute enthalpies at T2 from those at T1.
ΔHig = Habs,ig(T2) -Habs,ig(T1)
This gives the dark blue bars in the lower right diagram of Figure 1.
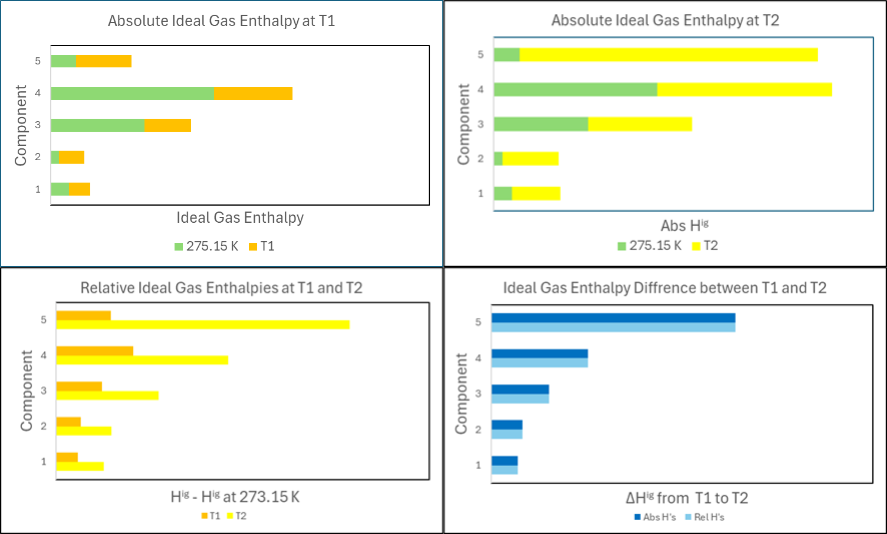
Since the absolute ideal gas enthalpies are difficult to evaluate, ideal gas enthalpies relative to a reference temperature, Tref, are preferred in engineering heat transfer calculations as illustrated in the lower left diagram of Figure 1:
Hrel,ig(T) = ΔHig(Tref -> T)
The light blue bars in the lower right diagram show the difference between the relative ideal gas enthalpies at the two temperatures. The enthalpy difference is the same independent of whether absolute or relative enthalpies are used because the composition is the same at T1 and T2.
As illustrated by the green colored bars in Figure 1, different components will have different ideal gas enthalpies at the reference temperature (here 273.15 K). In a petroleum reservoir, where the temperature and composition change with depth, the absolute ideal gas enthalpies of the individual components at the reference temperature will therefore contribute differently to the total absolute enthalpy at a temperature of T1 and at a temperature of T2. In such a system, it is not permissible to evaluate the ideal gas enthalpies relative to a reference temperature. Absolute ideal gas enthalpies are needed.
Although determining the absolute ideal gas enthalpy of a component is not straightforward, some qualitative differences are known. The ability of a hydrocarbon molecule to vibrate and rotate without moving its center of gravity increases with the number of single bonds between the carbon atoms, which results in an increased ideal gas enthalpy per mass unit. Figure 2 shows some examples of molecular structures. Methane consists of a single carbon atom bonded to four hydrogen atoms. This provides limited opportunities for intramolecular motions and thereby limits the specific absolute ideal gas enthalpy of methane. N-hexane has five single bonds between the six carbon atoms, which provides ample opportunities for internal vibrations and rotations. Benzene also has six carbon atoms, but they are connected by aromatic double bonds, which limits the possibilities for intramolecular movements and means that the absolute ideal gas enthalpy of benzene is lower than that of n-hexane.
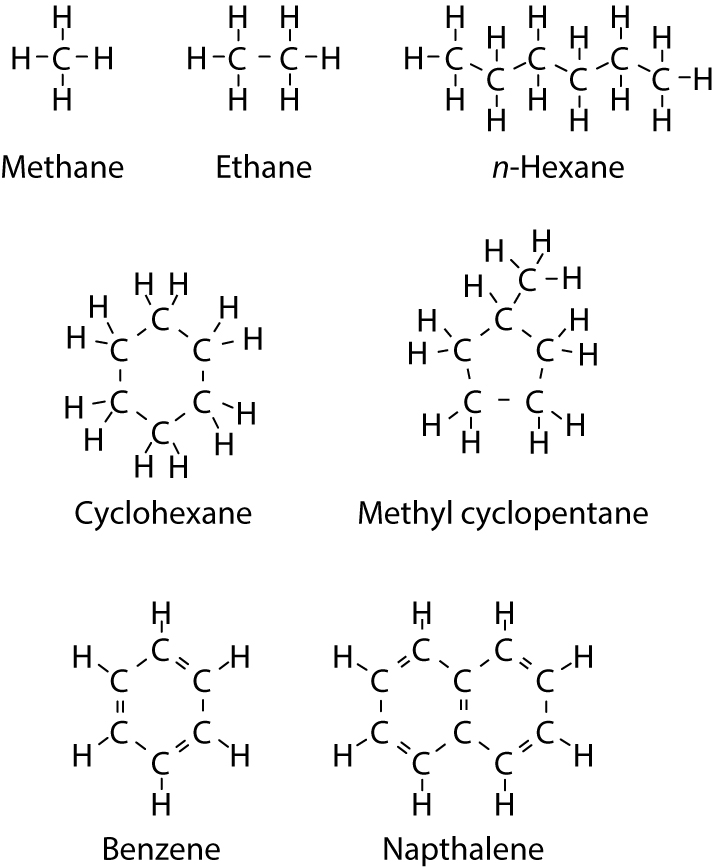
Figure 2 Constituents of petroleum reservoir fluids.
An accurate representation of how the fluid composition and the fluid properties evolve with depth is important as input to a compositional reservoir simulation. To move from qualitative considerations to quantitative depth gradient simulations, accurate absolute ideal gas enthalpies are needed.
Ideally, the absolute ideal gas enthalpies should be determined by placing a dilute gas mixture in a horizontal tube with a temperature gradient. This would develop a concentration gradient that, for each component, would be determined by the difference between its specific absolute ideal gas enthalpy and the average absolute ideal gas enthalpy of the entire mixture. However, on a laboratory scale, the concentration gradients are so small that it will be difficult to make precise measurements.
In a petroleum reservoir, the dimensions are so large that it is possible via fluid samples taken at different depths to get precise data for how the composition changes with depth. The parameters missing to make use of the Haase model are the absolute ideal gas component enthalpies at the reservoir temperature. The ideal gas enthalpies of the components relative to a reference state, here ideal gas at 273.15 K, can be evaluated from a polynomial in the absolute temperature. What remains is the ideal gas enthalpy of the individual components at the reference temperature of 273.15 K.
Kapexy has been fortunate to have access to an extensive data material for the variation in fluid composition with depth for reservoirs worldwide and with varying vertical temperature gradients. This has enabled us to map ideal gas reference enthalpies of all reservoir fluid components and to develop a powerful depth gradient simulation tool. If just a single fluid sample exists from a reservoir with a known temperature gradient, it is possible to simulate how the composition and GOR develop with depth and to simulate the depth of a possible gas-oil contact (GOC). If more fluid samples are available, data for these samples can be used to fine-tune the ideal gas enthalpies and get an exact match of an established GOC and how the GOR varies with depth. It is possible to assign higher weights to data of much importance. In addition to GOC and GOR, it could be saturation pressure profile and how the concentrations of certain components develop with depth.
The result of a depth gradient simulation for a field with a GOC and data for multiple fluid samples is illustrated in Figure 4.
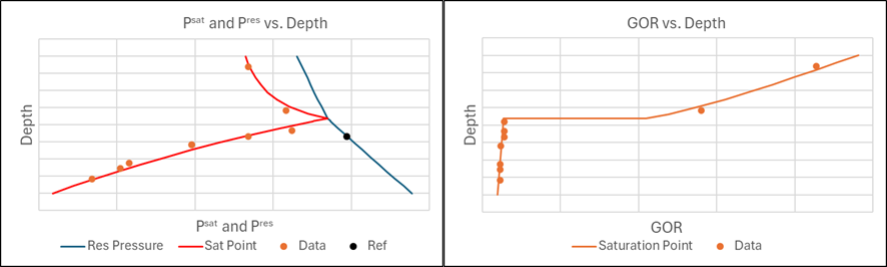
The described simulation tool is also applicable for reservoirs where the transition from gas to oil is smooth and the saturation pressure never reaches the reservoir pressure. Such cases are described in the technical note on Reservoirs with a Critical Zone.
References
[1] Haase, R., Thermodynamics of irreversible processes, Addison- Wesley, Reading, MA, 1969, Chapter 4.
[2] Schulte. A.M., Compositional variations within a hydrocarbon column due to gravity, SPE 9235, presented at the SPE ATCE, Dallas, September 21-24, 1980.
New Book on Phase Behavior of Petroleum Reservoir Fluids
Technical notes on Kapexy’s website usually address a specific technical issue. This note is an exception, by presenting the 3rd edition of the book on Phase Equilibria of Petroleum Reservoir Fluids written by Karen Schou Pedersen, Peter Lindskou Christensen, and Jawad Azeem Shaikh. Together the three authors have more than 100 years of practical and theoretical experience in this subject. The book covers a wide range of experimental techniques and simulation methods in its seventeen chapters. Below is a brief introduction to each chapter.
1 Petroleum Reservoir Fluids
The constituents of petroleum reservoir fluids are introduced. Reservoir fluids consist primarily of hydrocarbons ranging from methane with a single carbon atom to hydrocarbon compounds with more than a hundred carbon atoms. Reservoir fluids may also contain nitrogen, carbon dioxide and hydrogen sulfide. The difference in phase behavior between pure hydrocarbons and hydrocarbon mixtures is explained. There are different reservoir fluid types ranging from natural gases dominated by lighter hydrocarbons to heavy oils dominated by components with more than ten carbon atoms. Examples of each fluid type are shown. The most used terms to describe the phase behavior of reservoir fluids, such as critical pressure and temperature, acentric factor, dew point, and phase envelope, are explained.

2 Sampling, Quality Control, and Compositional Analyses
To carry out simulations of phase equilibria and physical properties for a reservoir fluid, it is necessary to have a representative sample and a compositional analysis of the fluid. The most used sampling techniques are presented as well as methods to ensure that the samples are representative of the reservoir fluid. It is explained how gas and liquids can be analyzed by gas chromatography and how a more elaborate liquid analysis can be established by a true boiling point analysis. Through calculation examples, it is explained how reservoir fluid compositions are established, based on compositional analyses of gas and liquid samples from a flashes of reservoir fluid or separator samples to standard conditions.
3 PVT Experiments
The PVT experiments the oil industry has adopted as a standard are presented. They cover the experiments carried out on the reservoir fluid (constant mass expansion, differential liberation, constant volume depletion and separator experiments) as well as experiments carried out on the reservoir fluid with added gas (swelling, equilibrium contact, multi-contact, slim tube, and gas revaporization). The latter experiments are primarily carried out for fluids from reservoirs, for which it may be relevant to carry out gas injection to increase the recovery. Examples are given of experimental data for each type of PVT study. The material balance tests carried out for studies where material is removed are presented and it is outlined what equipment and experimental technique to apply to measure gas Z-factors accurately.
4 Equations of State
Cubic equations of state remain a standard for PVT simulations in the oil and gas industry. These equations date back to the van der Waals equation presented in 1873. Currently the most used cubic equations are the Soave-Redlich-Kwong and Peng-Robinson equations. Both are to be used with a volume correction to simulate accurate liquid densities. Non-cubic equations may be used for specialized purposes. The PC-SAFT equation was developed for polymers but is also applicable to oil mixtures. The GERG-2008 equation was developed to provide more accurate simulation results for natural gas mixtures than cubic equations and can be used for mixtures with hydrocarbons up to C10. Very accurate property simulations for pure CO2 can be achieved with the Span-Wagner equation.
5 C7+ Characterization
Petroleum reservoir fluids contain thousands of different components, and it is impossible to analyze all of them. The components lighter than C7 can be quantitatively identified while the fractions C7 and heavier are divided into boiling point cuts where each cut may contain several components. Today’s compositional analyses most often stop with a C36+ fraction containing C36 and heavier. The plus fraction may have components as heavy as C200. To perform equation of state calculations, the plus fraction must be split into carbon number fractions and equation of state parameters assigned to each fraction (Tc, Pc and acentric factor) using correlations in molecular weight and density. Some fractions must be lumped together into pseudo-components to have a manageable number of components to work with in the subsequent PVT simulations. The term C7+ characterization is used for the described preparation of a reservoir fluid for equation of state calculations.
6 Flash and Phase Envelope Calculations
A flash algorithm is needed to make use of an equation of state to predict the conditions at which a fluid splits into two or more phases and the quantities and compositions of each phase. The equations that define a flash problem are presented, as well as the methods for determining phase quantities and compositions at thermodynamic equilibrium. Also covered are the techniques for handling aqueous and pure solid phases in flash calculations. The techniques for determining a gas-liquid phase envelope are outlined as well as criteria for distinguishing between a gas and a liquid phase in the supercritical region.
7 PVT Simulation
Simulation of experimental PVT data is an important part of equation of state modeling. If the simulation results do not agree well with the experimental data, it signals that something is wrong with the fluid characterization. Examples of simulation results are presented for the PVT experiments covered in Chapter 3. It is shown that an inaccurate plus molecular weight can degrade PVTsim simulation results and how this can be corrected for. Z-factor simulation results for a natural gas are shown with various equations of state including the GERG-2008 equation and compared with experimental data. Simulation results are shown for the concentration of mercury that can occur in a natural gas in contact with free mercury.
8 Thermal Properties
Enthalpy and entropy are explained based on the considerations that were behind the definition of these properties. They have a contribution from intermolecular interactions and another from the intramolecular energy possessed by the individual molecules. The former contribution can be calculated from an equation of state, while the latter one must be calculated empirically. It is explained how a well test can be used to determine the Joule-Thomson coefficient of a reservoir fluid if the reservoir temperature is known, and how the reservoir temperature can be determined if it is uncertain, but the Joule-Thomson coefficient is known. Simulated gas phase Joule-Thomson coefficients are compared with experimental data. Heat capacity and velocity of sound are also introduced.
9 Regression to Experimental PVT Data
Since it is not possible to make a complete component analysis for reservoir fluids, there is always an uncertainty regarding the composition of a such fluid. When reservoir fluid phase behavior is to be modeled with an equation of state, this uncertainty is eliminated by tuning to measured PVT data. This tuning must be carried out in such way that it is ensured that not only the measured PVT data is matched, but also that the model parameters are valid at other conditions and if gas is added to the reservoir fluid with the aim of achieving an enhanced recovery. The importance of matching the critical point of the fluid is emphasized.
10 Transport Properties
The transport properties, viscosity, thermal conductivity, interfacial tension, and diffusion coefficients are covered. In connection with reservoir simulation studies, it is especially the viscosity that is of interest, while all the mentioned transport properties are important in simulation of pipeline transport. For viscosity and thermal conductivity, the most reliable models are based on the corresponding states principle. Also presented is the LBC viscosity model, which has gained widespread use by being simple and easy to tune on. The experimental technique for measuring gas-oil interfacial tension is presented with correlations for calculating the interfacial tension. Transport property data are shown with corresponding simulation results.
11 Wax Formation
Heavy paraffinic compounds contained in reservoir fluids may precipitate as a solid wax phase if the fluid is cooled. Wax precipitation in a pipeline transporting an oil or a gas condensate will increase the viscosity of the liquid phase, and a wax layer may build up on the inside of the pipeline. Data is presented for wax precipitation from both stable oils and live oils. Modeling of wax precipitation from a reservoir fluid requires division of the C7+ components into potentially wax forming and non-wax forming compounds. The wax forming compounds must be assigned a melting temperature and a heat of fusion (melting) to represent the phase transition from liquid to wax. The amount of precipitated wax can be reduced by adding wax inhibitors, the most common of which are presented.
12 Asphaltenes
Asphaltene precipitation from reservoir oils may possibly occur in a pressure interval around the bubble point pressure. The precipitate is a highly viscous and sticky material that may cause deposition problems in production wells and pipelines. Asphaltene precipitation is increased if gas is added. Since experimental asphaltene studies are quite expensive, it may be attractive to use a screening method to clarify whether a reservoir fluid is at risk of causing asphaltene problems. Since paraffinic components are poor solvents for asphaltenes, paraffinic reservoir fluids are the most problematic even if the asphaltene content is low. With an appropriate choice of critical properties and binary interaction parameters for the asphaltene fraction, asphaltene precipitation can be modeled with a cubic equation of state.
13 Gas Hydrates
When transporting reservoir fluids carrying water at temperatures below 35°C, there is a risk of gas hydrates forming. These are solid structures consisting of water lattices stabilized by gas molecules. The physical appearance resembles that of snow and ice. Formation of gas hydrates may lead to plugging of pipes and process equipment. There are accurate models for predicting the pressure and temperature conditions at which gas hydrates can form. If pipeline transport takes place under conditions where hydrates can form, it is common practice to add a hydrate inhibitor. The most used are methanol and mono ethylene glycol. Salt is often contained in the formation water produced with a reservoir fluid and will also act as inhibitors.
14 Compositional Variations with Depth
The composition changes with the depth in a petroleum reservoir. The concentration of heavy components increases with depth. This is partly due to the action of gravity and partly to the vertical temperature gradient that exists in most petroleum reservoirs. Both effects will increase the compositional gradient and can be modeled by coupling transport of heat and mass using the concept of irreversible thermodynamics. For highly viscous fields, there is a need for a viscosity correction. In a gas zone, an increased content of heavy components will make the saturation pressure increase with depth. If the saturation pressure and reservoir pressure coincide, there will be a gas-oil contact, where the fluid composition changes discontinuously from gas to oil. If the saturation pressure remains lower than the reservoir pressure, the fluid type may instead change continuously from gas to oil by passing through a critical point.
15 Minimum Miscibility Pressure
Gas injection is an effective technique for obtaining an enhanced recovery from an oil field. The gas can be a hydrocarbon gas or CO2. Gas injection is most effective with a miscible displacement where the gas does not bypass the oil to create a gas breakthrough. A miscible displacement is achieved by a series of contacts between gas and oil, where the two phases exchange components to eventually become identical at a critical point. The lowest pressure for which a miscible displacement can be achieved is called the minimum miscibility pressure or simply the MMP. The MMP can be calculated analytically by a tie-line method, or it can be calculated by simulating the slim tube experiment used to experimentally determine the MMP.
16 Formation Water and Hydrate Inhibitors
Well streams often carry water from an underlying water zone, which calls for models that can simulate the mutual solubility of the water and hydrocarbon phases and the properties of the water phase. Due to strong intermolecular interactions, water cannot be handled using a cubic equation of state with classical mixing rules. The cubic equation must either use an advanced mixing rule as proposed by Huron and Vidal or have an additional association term (Cubic Plus Association) to represent the mutual solubility of water and hydrocarbons. The produced water phase will often contain salt, and if the well stream is to be transported in a pipeline, addition of a hydrate inhibitor may be needed. Suitable models to deal with these challenges are presented, as well as models for simulating the viscosity of water-oil emulsions.
17 Scale Precipitation
Produced well streams often carry formation water with dissolved salts from an underlying water zone. The solubility of some salts in water will be so low that they under certain conditions they will precipitate as a solid salt. Salt deposition is often referred to as scaling and is a potential problem in pipelines that transport unprocessed well streams carrying formation water. In the reservoir, scale precipitation can be seen when seawater is injected with the purpose of achieving an enhanced recovery. The solubility of a given salt can be derived from its solubility product. When more salts are present, their interaction will affect the solubility of the individual salts. This can be modeled using Pitzer’s activity coefficient model.
EoS Modelling with the Critical Point as Anchor Point
Summary
The phase behavior of a pure hydrocarbon is throughout the gas and liquid region essentially determined by the critical temperature and pressure of the component. Two recent Kapexy publications [1,2] show that the critical point also for a reservoir fluid exerts a large influence on the phase behavior of the fluid in the whole gas and liquid region. The critical point is so decisive for the behavior of a reservoir fluid that, in addition to the critical point, only a measured saturation point is needed to develop a reliable equation of state model. A measured critical point is rarely available for reservoir fluids, but the critical point of an oil can be calculated from the composition of the fluid. The same applies to the critical point of the C7+ fraction of a gas condensate. By utilizing this knowledge, the time spent developing equation of state models can be significantly reduced and performed with far less measured data than is standard today. There is the additional advantage that equation of state modeling can be performed as soon as a compositional analysis is available and does not have to await the full PVT study.
Theory
The famous Dutch scientist, van der Waals (vdW) presented the first cubic equation of state in 1873.
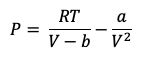
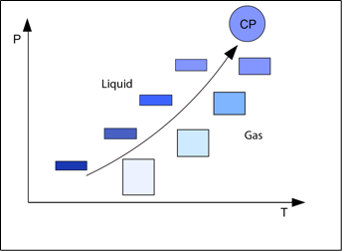
Figure 1 How van der Waals saw the development towards criticality for a pure hydrocarbon.
Today the industry standard cubic equations are the volume corrected Soave-Redlich-Kwong and Peng-Robinson equations. Unlike the van der Waals equation they can handle mixtures and therefore enable simulation of the critical point of a petroleum reservoir fluid.
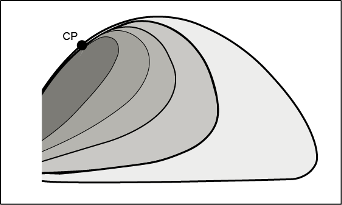
Figure 2 shows the phase envelope of a reservoir fluid with iso-volume (quality) lines. The quality lines are bound to meet at the critical point, and the location of the critical point exerts much influence on the phase amounts, properties, and compositions also at pressures and temperatures far from the critical point.
Figure 2 Phase envelope of a petroleum reservoir fluid with critical point (CP) and iso-volume (quality) lines.
Given that the location of the critical point affects the phase behavior of a reservoir fluid throughout the gas and liquid regions, and that the critical point is the basis of the cubic equations, one may wonder why the critical point of a reservoir fluid is not assigned importance in equation of state (EoS) modeling. The focus is instead on matching PVT data (CME, CVD, Differential Liberation, etc.) measured at the reservoir temperature. A likely explanation is that the PVT studies that are standard today were defined at a time when it was not possible to simulate the critical point of a multicomponent mixture. Calculation of the critical point of multicomponent mixtures and flash calculations in the near-critical region only became possible with Professor Michael Michelsen’s pioneering work within phase equilibrium algorithms in the early 1980s [3].
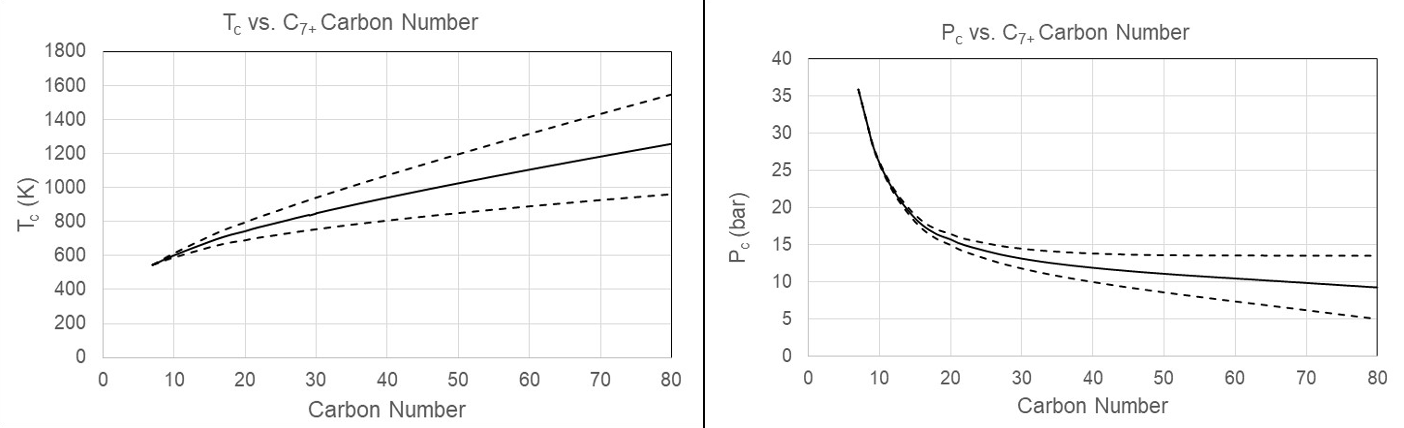
EoS modeling consists of representing the C7+ fraction of a reservoir fluid as an appropriate number of pseudo-components and assigning values of Tc, Pc and acentric factor to each of the C7+ components. Petroleum reservoir fluids are not random mixtures. The logarithm of the mole percentages of the C7+ components develop linearly with carbon number. This pattern is the result of chemical reactions that have taken place over thousands of years. The critical temperature of the components contained in the C7+ fraction increases with carbon number and the critical pressure decreases. As illustrated in Figure 3, EoS modeling can therefore be simplified to rotating the curves representing the standard development of Tc and Pc with carbon number around a fixed value of C7 until the target PVT data is matched.
Figure 3 Development of Tc and Pc with carbon number for C7+ fractions. The full drawn lines show the default developments. The dashed lines show the variation accepted during EoS model development.
Gas Condensates
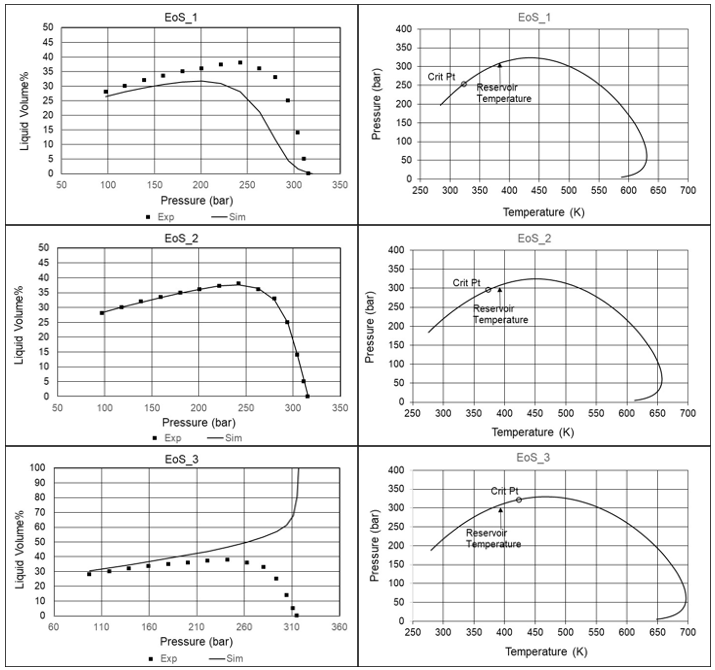
Those involved in equation of state (EoS) modeling for gas condensates will be familiar with the situation where the saturation point of the reservoir fluid is easily matched but the liquid dropout curves are not. The problem is exemplified in the left-hand side of Figure 4, which shows the experimental liquid dropout curve for a gas condensate as well as the liquid dropout curves simulated with three different EoS models, all of which match the saturation pressure. With EoS_1, the simulated liquid dropout curve is too flat. A perfect match is seen with EoS_2, while with EoS_3 the saturation pressure is simulated to be a bubble point instead of a dew point. The reason the liquid dropout curves differ is to be found in different simulated critical points. As can be seen from the phase envelope plots on the right-hand side of Figure 4, with EoS_1, the fluid is simulated to have a critical temperature much lower than the reservoir temperature. With EoS_2, the simulated critical temperature is still lower than the reservoir temperature, but not by much. Finally, the simulated critical temperature with EoS_3 is higher than the reservoir temperature. The simulated saturation point at the reservoir temperature is a bubble point and the fluid would erroneously be classified as an oil.
Figure 4 The left-hand side shows experimental and simulated liquid dropout data for a gas condensate fluid. The simulated liquid dropout curves are for three different EoS models. The right-hand side shows phase envelopes and critical points simulated using each of the three EoS-models.
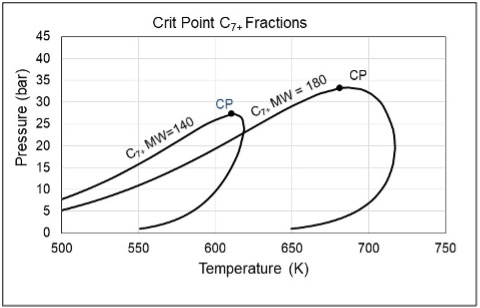
Kapexy has performed an analysis of a large number of gas condensate EoS models, all of which provided a good match of liquid dropout data measured in constant mass expansion and constant volume depletion experiments [2]. As illustrated in Figure 5, the critical temperature and critical pressure of the C7+ fraction were found to increase with the average molecular weight.
Figure 5 Simulated phase envelopes for the C7+ fractions of two gas condensates exemplifying the trend that the critical temperature and the critical pressure increase with average molecular weight of the C7+ fraction.
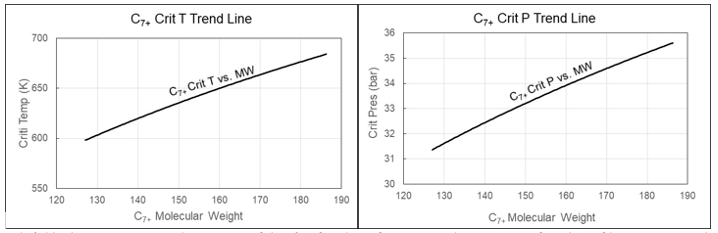
Correlations were developed for predicting the critical point of the C7+ fraction of a gas condensate from its average molecular weight [2]. These correlations are graphically illustrated in Figure 6.
Figure 6 Critical temperature and pressure of the C7+ fraction of a gas condensate as a function of its average molecular weight.
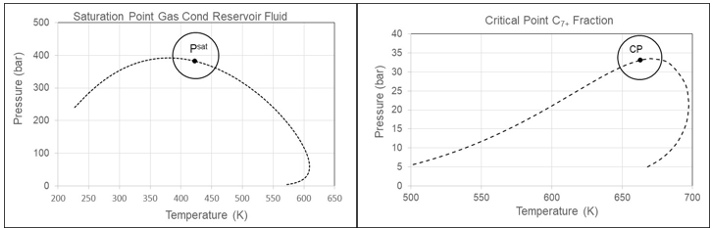
For any gas condensate fluid, it is now possible from Figure 6 to read off the critical temperature and the critical pressure of the C7+ fraction based on its average molecular weight. If a measured saturation point exists for the entire fluid, the information in Figure 7 is available. Subsequently, the Tc and Pc curves in Figure 3 are rotated around the values for C7 until the simulation results agree with the data in Figure 7. The result can be as shown in Table 1 and as exemplified for this fluid in Figure 8, this will normally give a good agreement with the measured liquid dropout curves.
Figure 7 Data points deciding the phase behavior of the gas condensate reservoir fluid in Table 1.
Table 1 Gas condensate reservoir fluid for which the C7+ fraction has been characterized to match data in Figure 7. Experimental and simulated liquid dropout curves can be seen from Figure 8.
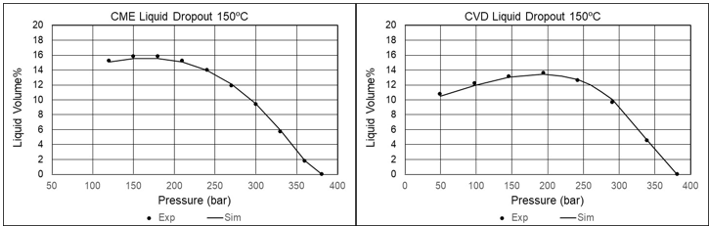
Figure 8 Experimental and simulated CME and CVD liquid dropout curves for the gas condensate mixture in Table 1, which has an average C7+ molecular weight of 165.
Oil Mixture
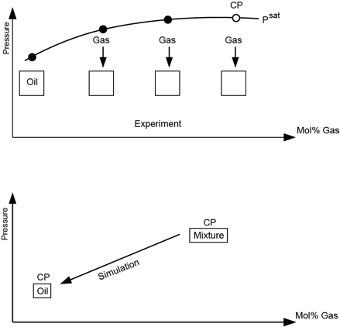
A swelling experiment stands out among PVT experiments. It is performed at the reservoir temperature and starts with a measurement of the saturation point of the reservoir oil. Gas is added in steps, and after each gas addition, the saturation pressure is measured. It is further recorded when the saturation point changes from a bubble point to a dew point. Between the last bubble point and the first dew point is a composition that is critical at the saturation pressure. If the equation of state parameters are tuned to match that this composition is critical, it allows the critical point of the reservoir oil to be determined as is illustrated in Figure 9. This is done using the same EoS model to simulate the critical point of the fluid after having removed the added gas. The components in the added gas have well-defined equation of state parameters, and the assumption is that these components are correctly described both in the critical fluid composition with gas added and in the reservoir fluid before adding any gas.
Figure 9 How to determine the critical point of a reservoir oil
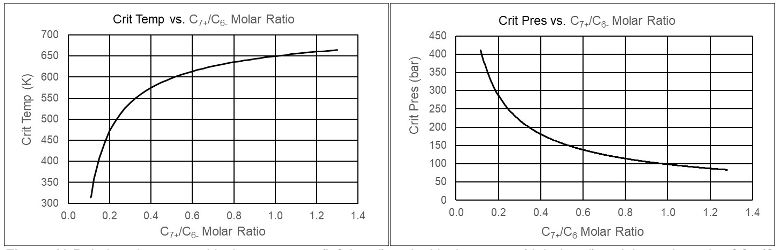
Swelling experiments are quite costly and will rarely be conducted unless gas injection is considered as an increased recovery technique. Fortunately, sufficient swelling data has been published to allow correlations to be developed for predicting how the critical temperature and pressure of a reservoir oil evolve with the C7+/C6- hydrocarbon molar ratio. This development is shown graphically in Figure 10 and is valid for reservoir fluids for which at least 10 mol% of the hydrocarbons are C 7+ components.
Figure 10 Relations between critical temperature (left-hand) and critical pressure (right-hand) and the molar ratio of C7+/C6- hydrocarbons for a reservoir oil composition.
The EoS modeling procedure, utilizing the found relationship between the critical point and the C7+/C6- hydrocarbon molar ratio, is as follows for reservoir fluids for which at least 10 mol% of the hydrocarbons are C7+ components [1].
- Make a copy of the fluid and remove inorganics (N2, CO2 and H2S).
- Calculate the molar C7+/C6- hydrocarbon ratio for the fluid from 1.
- Read off from Figure 10 the critical temperature and pressure for the fluid from 1.
- Rotate the Tc and Pc curves in Figure 3 to match the measured saturation pressure of the reservoir fluid and the critical point from 3. of the reservoir fluid freed of inorganics.
- Use the resulting EoS model for the reservoir fluid. It is applicable at both reservoir and process conditions as well as when gas injection is used as an EOR technique.
References
[1] Pedersen, K.S., Shaikh, J.A. and Christensen, P.L., Importance of critical point for the phase behavior of a reservoir fluid, Fluid Phase Equilibria 573, 2023.
[2] Pedersen, K.S., Christensen, P.L. and Shaikh, J.A., Use of critical point in equation of state modeling for reservoir fluids, SPE-216776-MS, Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, October 2-5, 2023.
[3] Michelsen, M.L., Calculation of phase envelopes and critical points for multicomponent mixtures, Fluid Phase Equilibria 4, 1980, 1-10.